今天, 我们要讨论一个十分常见且有趣的算法: 压缩. 相信大家遇到过下载资源时或多或少都碰到过压缩包吧, 但不知道大家有没有思考过它们是如何工作的? 为什么能将压缩包这个比较小的文件转换成原来的大文件, 且大文件也没有损失呢? 在这篇文章中, 我将讲解压缩算法的基本原理, 并讨论一些压缩理论中让我十分感兴趣的部分.
概论
在计算机中, 所有信息都是用0和1表示的. 我们可以用一个字节(8个二进制位)表示一个ASCII字符. 然而, 在一个文本文件中, 我们可能不会用到其中所有的字符, 因此我们可以通过用更短的二进制串表示一个字符.
然而, 仅仅这样也是不够的. 让我们来考虑一个摩尔斯电码的例子吧. 在摩尔斯电码中, 有 $\cdot$ 和 $-$ 两种符号, 这与我们的计算机十分相似.

而且, 摩尔斯电码中最长的字符也只有5个符号, 比一个ASCII码要短. 那我们能不能干脆用摩尔斯电码作为一种压缩算法呢?
要是你有这种想法, 不妨考虑这样一个问题: 请翻译 $–\cdot –\cdot$ . 对照摩尔斯电码表我们可以发现, 这段摩尔斯电码有多种可能: “GG”, “MEME”, … 在现实使用过程中, 我们可以通过在字与字之间添加停顿来达到区分的目的, 但是这样实质上是使用了三种符号( $\cdot$ , $-$ 和停顿), 在计算机中并不能够实现.
因此, 我们希望在我们压缩后的编码中, 不存在一个字符的压缩码是另一个字符的前缀. 这样, 当我们识别出一个字符后, 我们就能够确保这段二进制串就是代表这个字符, 而不可能和后面的一段二进制串共同组合成一个其他字符. 我们称这样的编码是前缀不重复的.
举个例子来说: “A: 0, B: 10, C: 11”是一个前缀不重复编码, 因此二进制串”01011”能被唯一转化成”ABC”;
“A: 0, B: 01, C: 10”不是一个前缀不重复编码(A是B的前缀), 因此二进制串”010”既可能是”AC”, 也可能是”BA”
因此, 一个压缩算法的目的就是找到一个前缀不重复编码, 并按照该编码将源文件转化为一个压缩文件. 在解压缩时, 我们只需要对照同一套编码遍历压缩文件, 就能恢复得到源文件.
我们会发现, 这套编码中每个字符是允许二进制表示的长度不一样的, 那么, 为了尽可能压缩文件, 我们还希望保证出现频率较高字符的二进制表示较短.
举个例子: 我们有这样一段文字: “AAAAAAAAAB”, 比较以下两种编码方式:
- “A: 0, B: 10”: 压缩文件是: “00000000010”, 其长度是11.
- “A: 01, B: 1”: 压缩文件是: “0101010101010101011”, 其长度为19.
那么, 怎么才能找到这样一套编码系统呢?
香农-范诺编码
香农-范诺编码是一套前缀不重复编码体系. 其编码步骤为:
- 统计每种字符的出现频率
- 将这些字符分为两组, 使每组字符的频率之和大致为0.5.
- 对每组字符重复步骤1, 直到一组只包含一个字符为止.
对于以下文件:
| 字符 | 频率 |
|---|---|
| A | 0.35 |
| B | 0.16 |
| C | 0.17 |
| D | 0.17 |
| E | 0.15 |
编码的可视化过程如下:
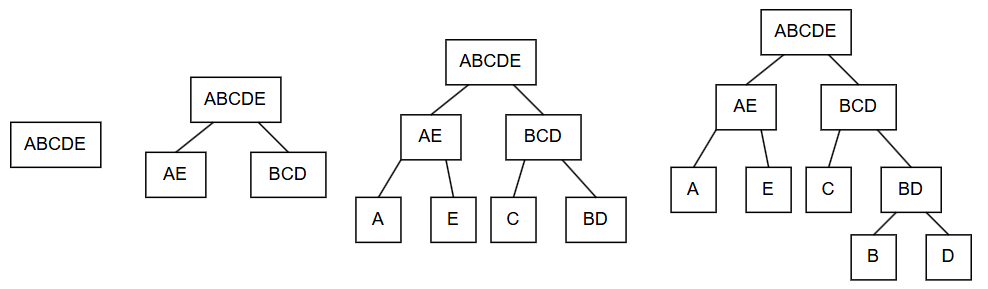
最终, 我们得到了一棵二叉树(每个节点最多有两个子节点的树). 我们可以规定这棵树中所有左枝为0, 右枝为1, 则得到编码: “A: 00, B: 110, C: 10, D: 111, E: 01”.
可以发现, 由于所有的字母都是树的叶节点(没有子节点的节点), 因此不可能有一个字符的编码是另一个字符编码的前缀, 因此该编码是前缀不重复的.
假设该文件中有100个字符, 则该编码可以将原来的文件($8 \times 100 = 800$位)压缩成为一个
\[35 \times 2 + 16 \times 3 + 17 \times 2 + 17 \times 3 + 15 \times 2 = 233\]位的压缩文件. 好棒呀!
但是我们能不能做得更好呢?
哈夫曼编码
在香农-范诺编码的基础之上, 哈夫曼发明了一套自下而上的编码系统. 其步骤为:
- 统计每种字符的出现频率.
- 从所有符号中, 选择出现频率最低的两个符号, 并且组合成一个新的符号, 其出现频率为两个符号之和.
- 重复第二步, 直到只剩下一个符号为止.
对于香农-范诺编码中的例子, 哈夫曼编码过程如下:
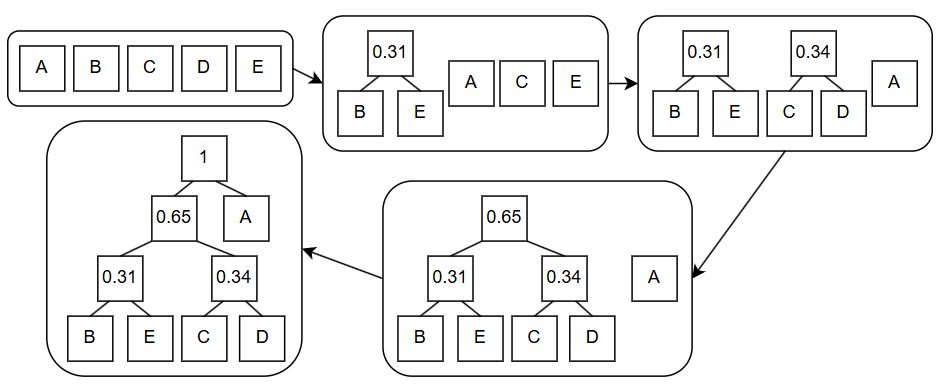
同样的, 我们将左枝视为0, 右枝视为1, 可以得到以下哈夫曼编码: “A: 1, B: 000, C: 010, D: 011, E: 001”.
到底哪种编码方式更好呢? 对于一个100个字符的源文件, 使用哈夫曼编码得到的压缩文件长度为:
\[35 \times 1 + 65 \times 3 = 230\]事实上, 哈夫曼编码是最优的压缩算法.
压缩理论
这么来看, 压缩应该很容易吧? 要理解这个问题, 不妨让我们考虑一下压缩的本质. 压缩实质上是用一个短的二进制串表示一个长二进制串的完整信息.
让我们考虑一个压缩算法: 如果输入的是莎士比亚全集.txt, 则压缩为0位的二进制串(即一个空串); 若输入其他文件, 则输出原文件去除第一位. 这样, 我们就可以把莎士比亚全集压缩到0字节(甚至0比特)了! 这样一个压缩算法是一个好算法吗?
显然不是. 首先, 这个算法并不通用: 对于除了莎士比亚全集的其他文本, 并不能写出一个能够无损解压的算法. 其次, 对于莎士比亚全集, 解压算法中必须包含这本书的文本, 才能够将其输出. 因此, 该算法实质上将信息存贮在了解压算法中.
为了能够公平地评估一个压缩算法, 我们需要建立以下压缩模型:
压缩文件: 压缩后二进制串+解压算法 ---> 某个计算环境 ---> 源文件
也就是说, 压缩后的二进制串 + 解压算法的长度越小, 压缩算法越好.
从现在开始, 我们所讨论的压缩文件的含义就是压缩后的二进制串与解压算法二进制串之和. 直观的解释是, 这样的一个文件包含了我们复原文件所需的所有信息.
现在, 让我们再次考虑压缩的本质: 用一个短的二进制串表示一个长二进制串的完整信息. 一个n位的二进制串可能的组合有$2^n$种, 这也就意味着短的字符串能保存的信息一定是比长字符串少的. 对于一个n位的二进制串来说, 所有比它短的二进制串的可能性之和只有$2^n - 1$种, 这也就意味着至少有一个n位二进制串是无法压缩的.
在现实中, 解压软件包含了足够多的信息, 保障了大部分文件都可以”被压缩”. 但是要算上解压软件的大小, 这些压缩包的大小大都会比原来的大. 但是由于压缩算法是通用的, 其中的信息可以被不同文件重复利用, 因此实际上这也是一个解决压缩问题的方法.
实际上, 在我们所定义的压缩模型下, 一个能将所有文件压缩的算法是一个NP完全问题
在探索压缩问题的过程中, 有很多人提出了稀奇古怪的想法, 接下来我们将要讨论一个我认为十分有趣的想法: 可理解的压缩.
可理解的压缩
我刚刚使用代码创作了一个递归艺术画:
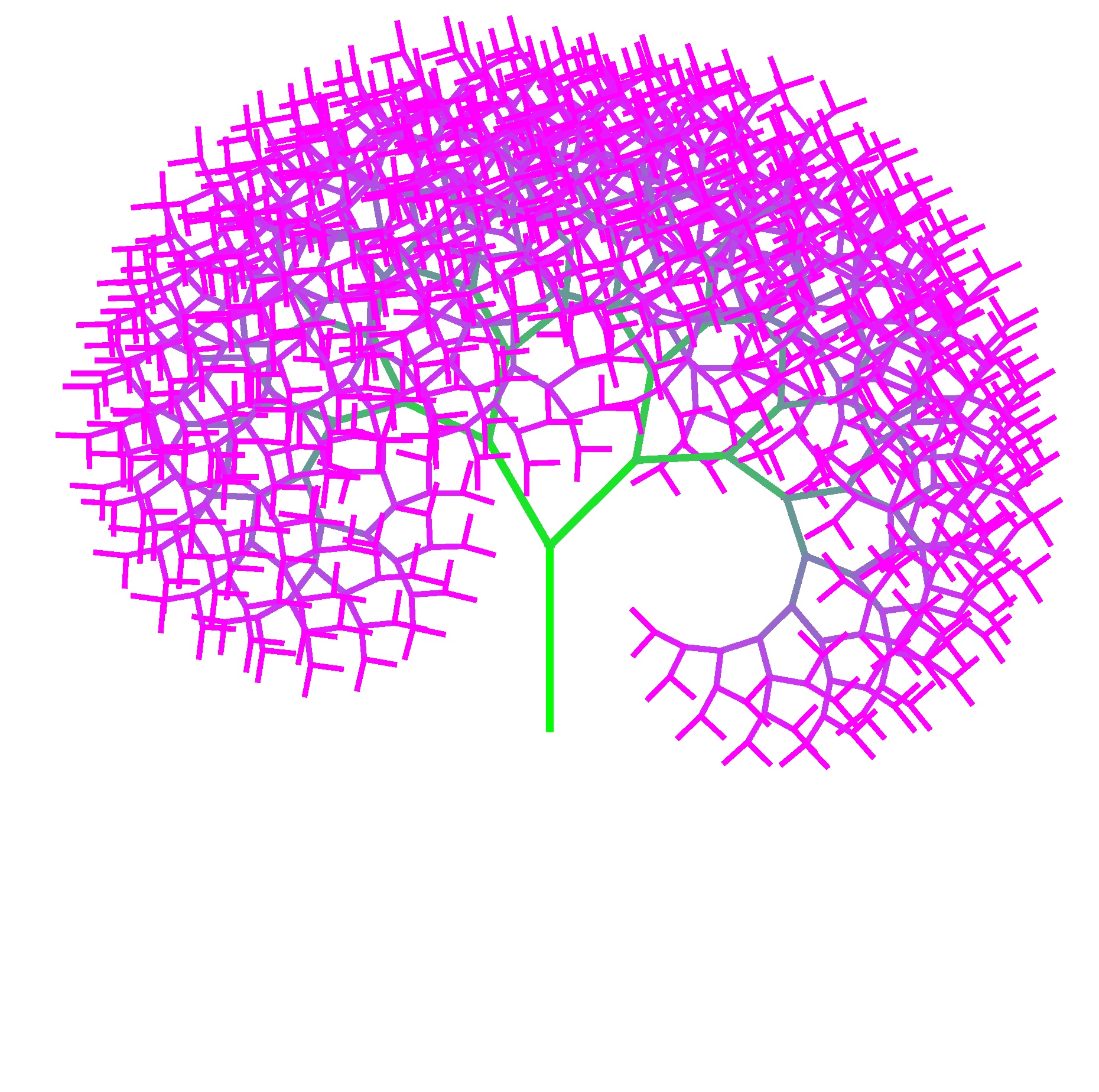
这个图片占用的空间是1,012,048字节. 使用7z对其进行压缩, 得到的文件大小为885,886字节. 但是, 要是我声称, 能够将这张图片压缩到1,830个字节, 大家会怎么想?
实际上, 我已经做到了, 而”压缩后的文件”就是生成这个递归画所需的代码.
那么, 有没有可能能够设计一个压缩算法, 使其能够输出一段代码, 而这段代码的输出就是源文件呢?
首先, 目前没有这样的算法, 这更多是一个思维实验.
Scott Aaronson认为, 如果我们能够将一些复杂的东西, 如股票市场或人类的基因, 压缩成为可理解的代码, 那么通过分析这些代码, 我们就能一窥这些事物的本质; 也就是说, 我们能压缩我们理解的事物, 而我们所理解的事物也是我们能够预测的.
- 对于我来说, 我认为这样的思想很好地诠释了我写这些文章(对我来说也是一种压缩)的初衷.
- 但是, 反对者认为, 代码不一定是可理解的.
我认为我对可理解压缩的阐述较为混乱(大概因为我也没有完全理解吧hhh). 但是我认为这样的一个思想是十分有趣的, 因此也在这里分享给大家, 感兴趣的可以阅读Scott Aaronson的原文.